Tal como contábamos en entregas anteriores, la creciente navegación comercial trajo acarreada la necesidad de una representación fidedigna de la superficie terrestre, tanto más importante cuanto mayores eran las relaciones y el comercio entre países distantes. Los mapas terrestres y las cartas náuticas se obtienen en su gran mayoría de “proyectar” alguna porción de la superficie terrestre sobre un plano de papel, o bien sobre alguna otra forma geométrica, seguido de algún desarrollo posterior. Se define como proyección a la figura que resulta de proyectar, en una superficie determinada, todos y cada uno de los puntos de una figura cualquiera.
Muchas de las cartas marinas que se utilizan en la actualidad se construyen proyectando la esfera terrestre sobre un plano. Si para ello se toman en cuenta superficies pequeñas (100 a 200 km2), la representación obtenida puede considerarse perfecta, ya que prácticamente no existen deformaciones propias de la curvatura terrestre. En el caso de representaciones de grandes territorios, las deformaciones son de consideración ya que el intentar desarrollar una esfera sobre un plano, de forma tal que ambos coincidan exactamente, se torna absolutamente imposible. Veamos algunas formas de resolverlo.
LAS DISTINTAS PROYECCIONES
Si bien las cartas náuticas o los mapas terrestres se pueden clasificar de miles de maneras diferentes, la única clasificación que interesa a nuestros fines es aquella que se basa en la “forma” en que se obtiene la proyección, y dentro de esta categoría podemos diferenciar a tres grandes grupos:
- Proyecciones puras: son aquellas que surgen directamente de proyectar la superficie terrestre sobre un plano o sobre una forma geométrica que más tarde se desarrolla a fin de convertirla en un plano. Las proyecciones puras se subdividen a su vez en tres grupos:
- Naturales o poliédricas.
- Por desarrollo.
- Proyecciones modificadas: son proyecciones que se obtienen a partir de modificar a alguna de las proyecciones puras con el objeto de mejorar ciertas particularidades que se precise utilizar. En realidad son proyecciones puras ligeramente modificadas.
- Proyecciones calculadas: las proyecciones calculadas están basadas en formulaciones matemáticas precisas que relacionan los puntos de la carta con los de la superficie terrestre a proyectar.
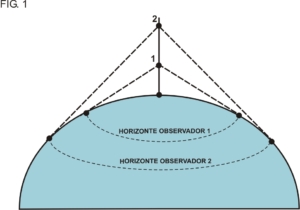
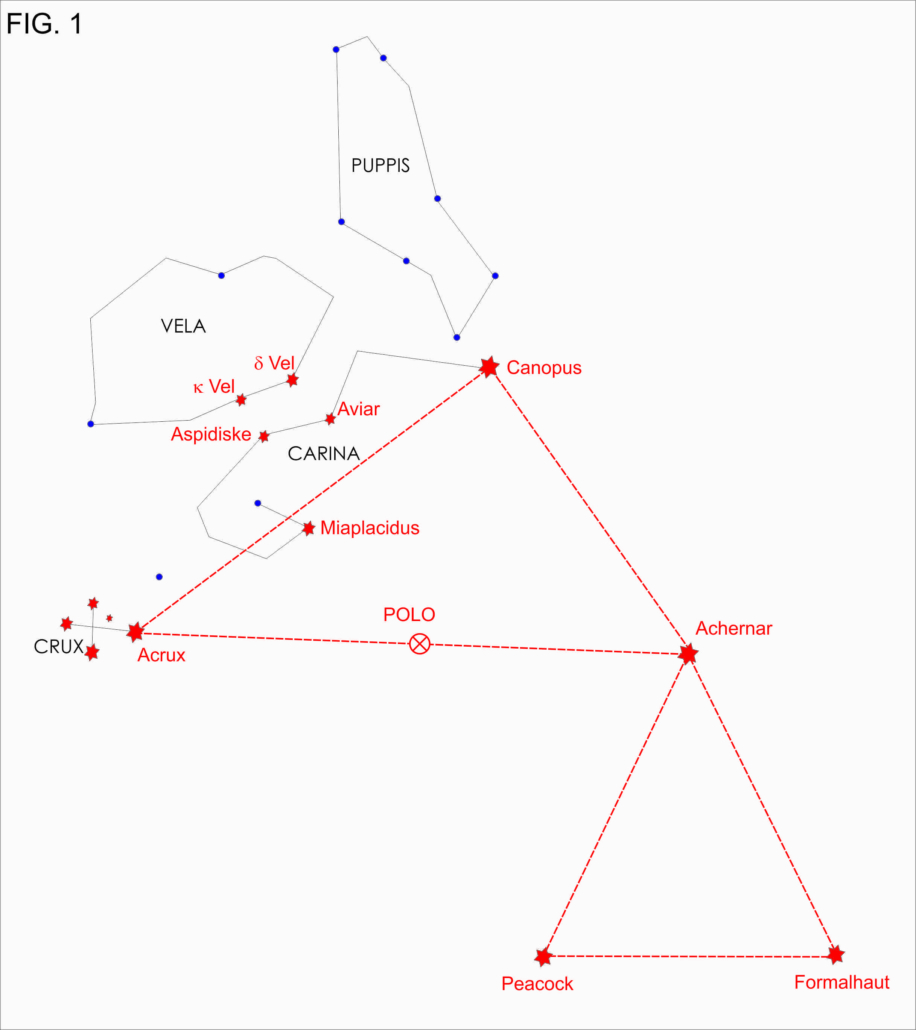
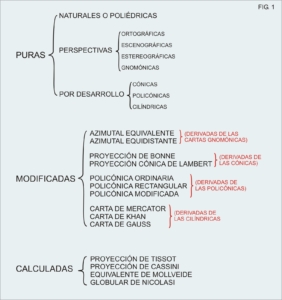
En la figura que Nº 1 podemos apreciar un resumen de las proyecciones más utilizadas:
Proyecciones naturales o poliédricas
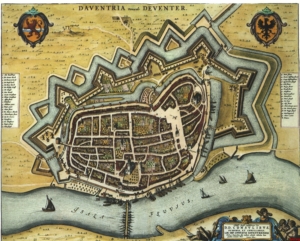
Las proyecciones naturales o poliédricas se utilizan mayormente para representar una pequeña superficie de la esfera terrestre y se caracterizan por reproducir muy bien el terreno comprendido dentro de la misma. Se utilizan en realidad para efectuar levantamientos topográficos más que para cartas náuticas, y surgen de superponer la porción de la esfera terrestre a representar a un plano tangente a su centro.
Proyecciones perspectivas
Este tipo de representaciones surgen de proyectar a la esfera terrestre directamente sobre un plano, sin necesidad de posterior desarrollo. Dentro de las proyecciones perspectivas podemos encontrar cuatro variantes, que dependen exclusivamente del punto de vista del observador:
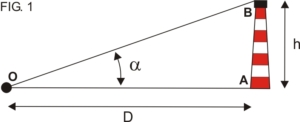
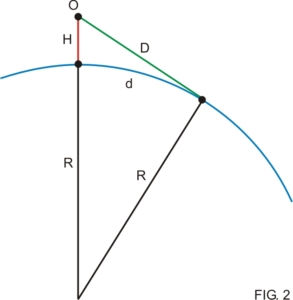
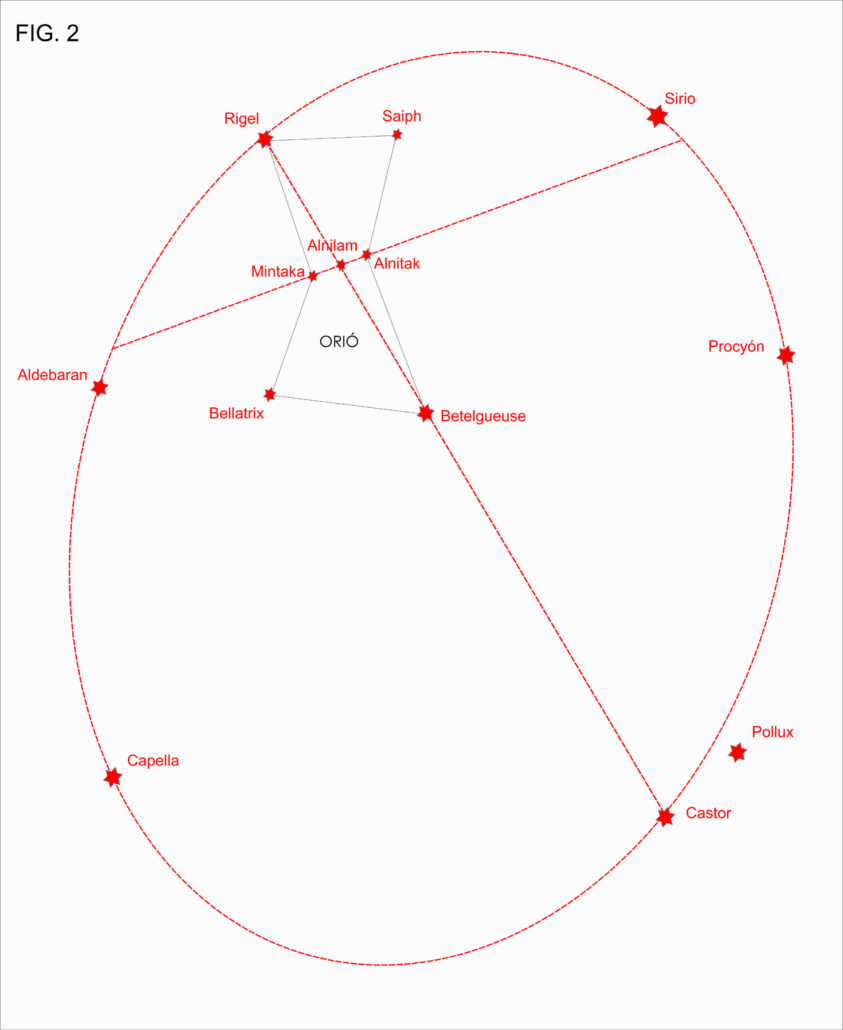
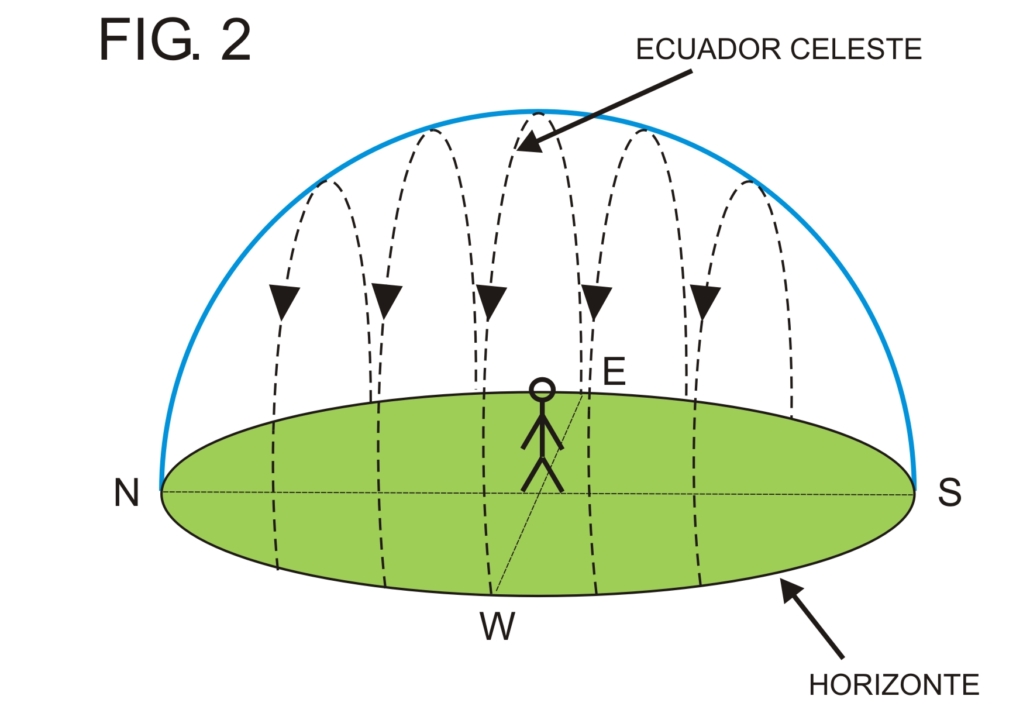
- Proyecciones ortográficas: En las proyecciones ortográficas el punto de vista del observador se encuentra por fuera de la esfera terrestre y a una distancia infinita de la misma. Sirve básicamente para mostrar la apariencia que tiene la tierra vista desde el espacio y no se utiliza en navegación ya que no muestra áreas reales por sufrir enormes distorsiones (Fig. 2).
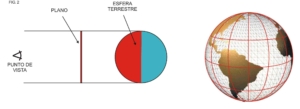
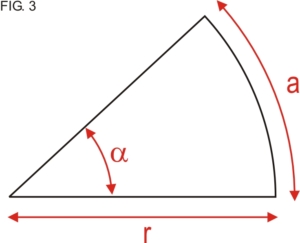
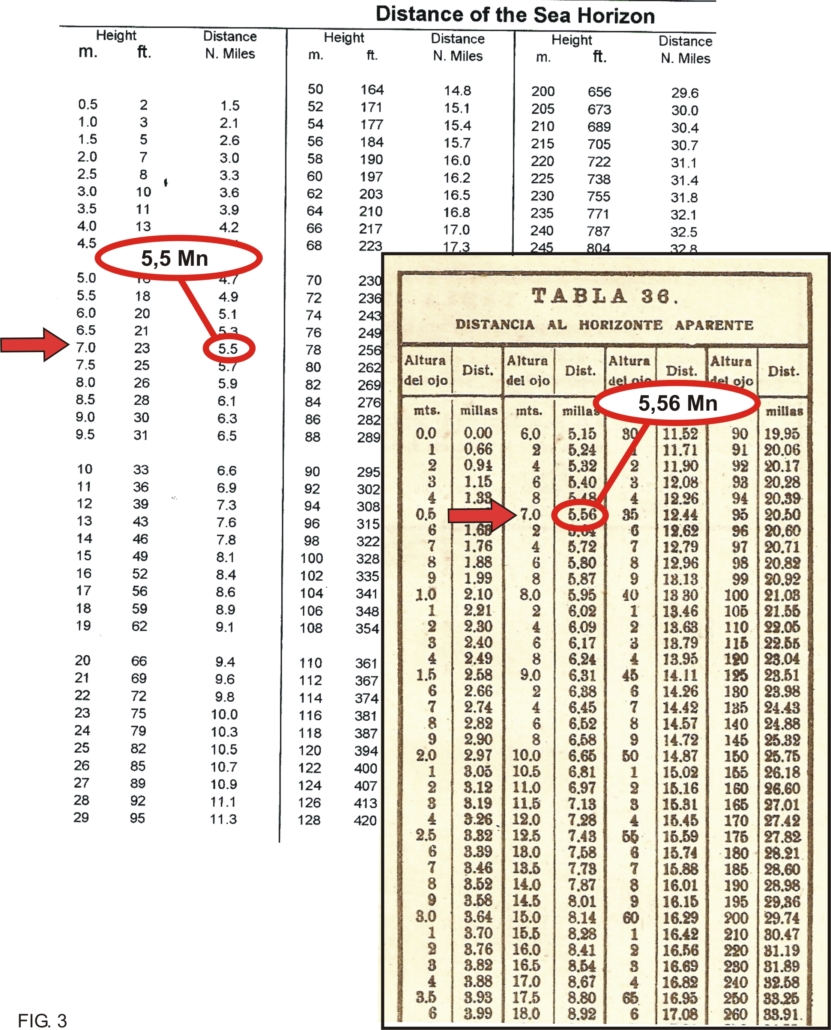
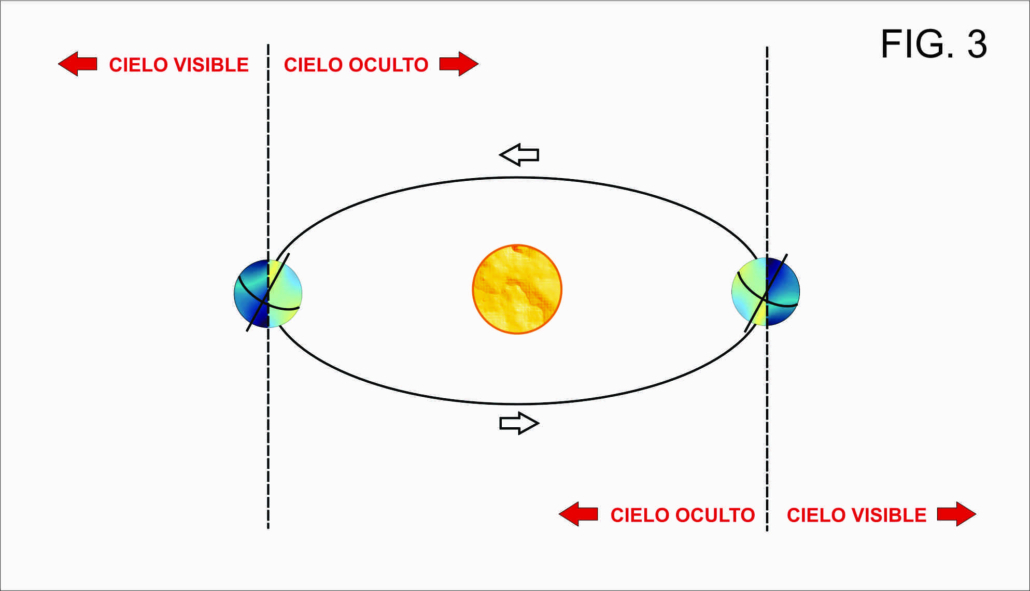
- Proyecciones escenográficas: Similares a la anterior, en este tipo de representación el punto de vista se ubica por fuera de la esfera terrestre pero a una distancia determinada (Fig. 3).
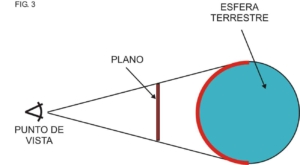
- Proyecciones estereográficas: En la proyección estereográfica, el punto de vista se encuentra sobre la esfera terrestre y en las antípodas del plano de proyección
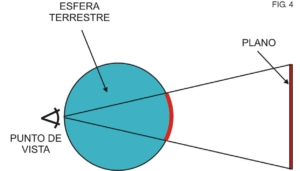
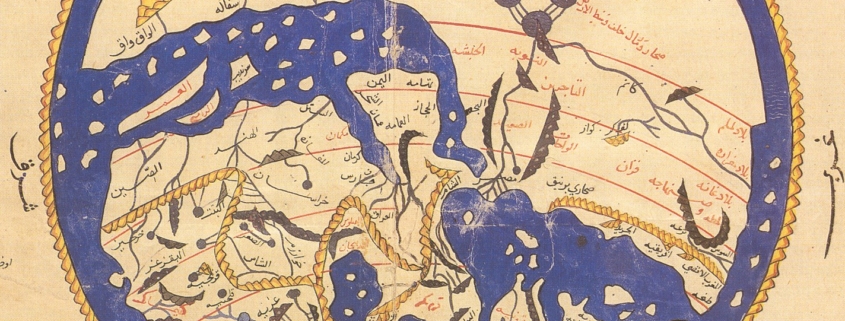
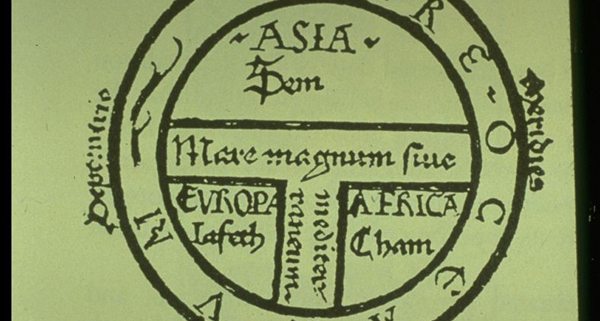
Según se sabe, las primeras proyecciones estereográficas que se conocen pertenecen a Ptolomeo y se encuentran publicadas en su célebre planisferio, aunque se supone que la idea original se atribuye a Hiparco (200 a.C.).
En realidad, el primer mapa conocido que utiliza este tipo de proyección pertenece a Johann Werner y representa a la ciudad de Nuremberg. Dicho mapa data del 1514.
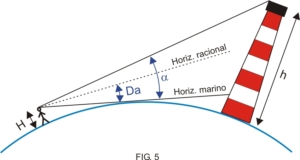
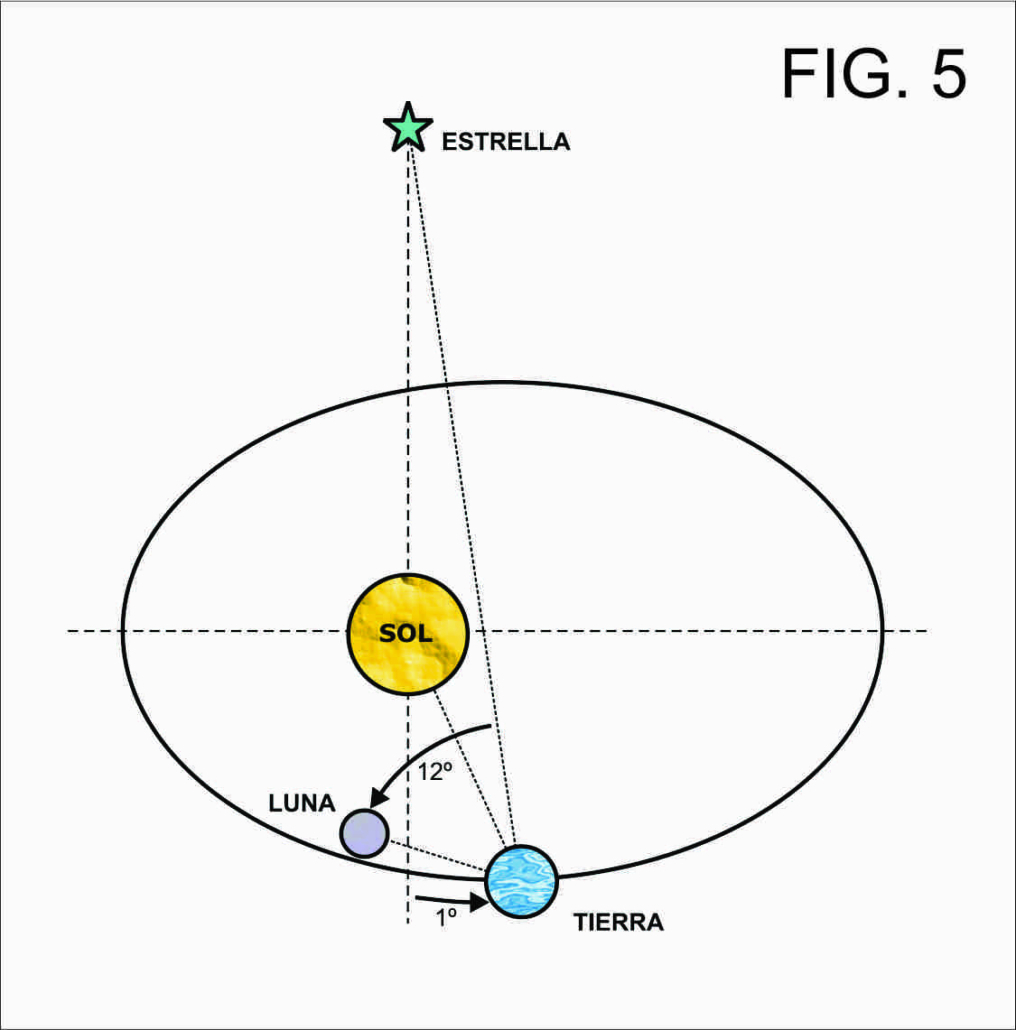
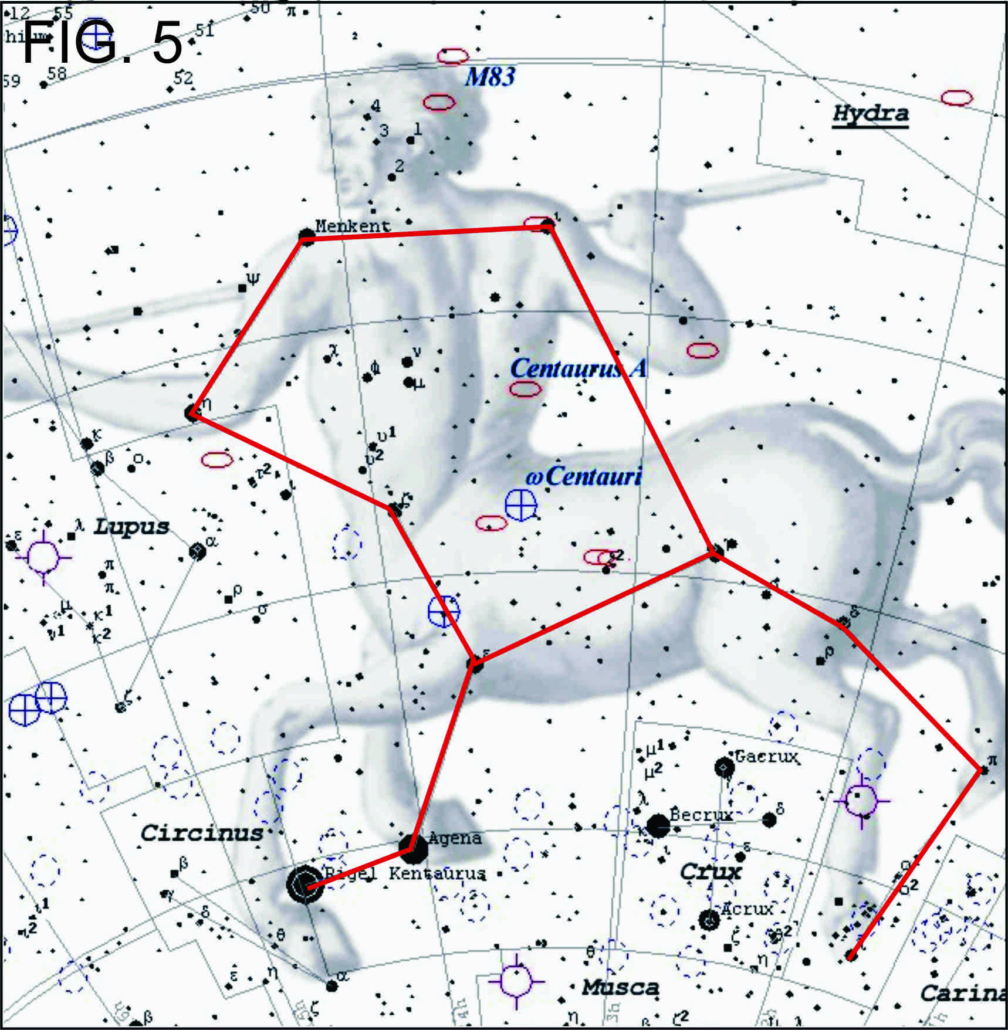
- Proyecciones gnomónicas: Surgen de ubicar al observador en el centro mismo de la esfera (centrográfica). El desarrollo de este tipo de proyección es atribuido a Thales de Mileto en el año 500 a.C. y continúa utilizándose en la actualidad para la navegación ortodrómica o por círculo máximo. La ventaja de este tipo de proyección por sobre las demás es que todos los círculos máximos se ven representados como líneas rectas. Esto es fácilmente comprensible si pensamos que cualquier círculo máximo contiene a la posición del observador, ya que éste se encuentra ubicado en el centro de la esfera (Fig 5).
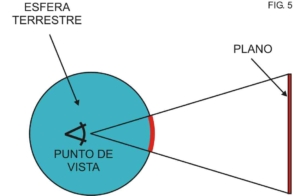
ESTEREOGRÁFICAS Y GNOMÓNICAS
De las proyecciones perspectivas las únicas utilizadas en navegación son las estereográficas y las gnomónicas, especialmente esta última ya que el uso de la estereográfica se limita solamente a regiones polares.
Una consideración a tener en cuenta es que, dependiendo de la posición del plano de proyección, estas representaciones pueden ser de cuatro tipos:
Meridiana: Cuando el plano de proyección es tangente a la esfera en el ecuador.
Ecuatorial: Cuando el plano de proyección coincide con el del Ecuador.
Polar: Cuando el plano de proyección es tangente a alguno de los polos.
Horizontal: Cuando el plano de proyección es tangente a un punto cualquiera de la esfera terrestre.
De lo anterior se desprende que, dependiendo de las necesidades particulares de cada navegación, las cartas a utilizar puedan ser: gnomónica meridiana, gnomónica polar, gnomónica horizontal, estereográfica meridiana, estereográfica ecuatorial, estereográfica polar y estereográfica horizontal.
Para zonas polares, si bien pueden utilizarse cartas con proyección gnomónica horizontal, es más frecuente el uso de gnomónicas polares. Las medidas de rumbos y distancias en este tipo de cartas suelen verse facilitadas por la inclusión de diagramas.
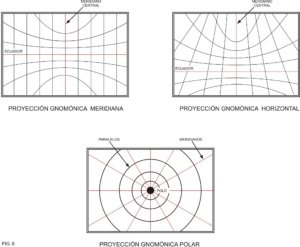
En la carta gnomónica meridiana, también conocida como carta “Hilleret”, tanto el Ecuador como el meridiano de tangencia son líneas rectas perpendiculares entre sí. El resto de los meridianos serán rectas paralelas al meridiano central, mientras que los paralelos resultarán hipérbolas con su concavidad hacia los polos.
En la proyección gnomónica polar, llamada también “carta alemana”, los meridianos serán radios del círculo que limita la proyección, mientras que los paralelos se verán representados como círculos concéntricos. La razón de esto es que el plano de tangencia se encuentra en alguno de los polos. La gnomónica horizontal, menos utilizada que las anteriores, sirve para representar a la zona que rodea al punto que se precisa proyectar, y sobre este punto se aplica el plano de tangencia. En ésta, los meridianos aparecerán como líneas inclinadas que convergen en alguno de los polos, pudiendo quedar el punto de convergencia (polo) por fuera de la carta. Aquí los paralelos se verán como trozos de parábola. En la figura Nº 6 pueden apreciarse con claridad las diferencias entre las tres variantes de proyecciones gnomónicas.
Las cartas estereográficas de uso más frecuente son las polares. Su característica principal es que todos los paralelos son círculos que se van separando cada vez más hacia el Ecuador, siendo este último el círculo exterior de la carta (Fig. 7).
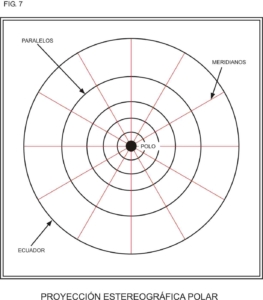
Ésta es en realidad la característica principal que distingue a la estereográfica polar de la gnomónica polar, ya que en esta última el ecuador no se encuentra representado. Esto se debe a que, como vimos, el punto de vista de las gnomónicas se encuentra en el centro del globo terráqueo, razón por la cual el Ecuador se proyecta en el infinito.
Proyecciones por desarrollo
Las proyecciones por desarrollo surgen de utilizar un cono, o bien un cilindro como planos de proyección, los que luego deberán desarrollarse para obtener un plano. De ahí su denominación. Según sea la figura geométrica utilizada, las proyecciones por desarrollo se dividen en tres grandes grupos:
- Proyecciones cónicas: Este tipo de proyección surge a partir de hacer coincidir al eje de un cono con algún diámetro de la esfera terrestre. Sobre la superficie de dicho cono se proyectan todos los puntos del globo y posteriormente se desarrolla el mismo.
En caso de que el eje del cono coincida con el eje de los polos, la proyección cónica resultante llevará el nombre de “directa”. Aquí, los meridianos se verán como líneas rectas que convergen en el polo, mientras que los paralelos serán círculos menores paralelos entre sí.
Si el eje del cono no coincide con el de los polos, la proyección resultante se llamará “transversa”.
Las proyecciones cónicas son muy útiles ya que dan lugar a numerosas variantes de proyecciones modificadas. Entre ellas, la más importante es la “proyección conforme de Lambert”. Esta última es muy usada tanto en aviación como en el ejército, aunque casi no se utilizan para navegación. La conforme de Lambert surge de proyectar los distintos puntos del globo hacia un cono, que es “secante” a la esfera en lugar de ser tangente a la misma (fig. 8). La ventaja de este tipo de proyección radica en que al penetrar algo el cono en la esfera se obtienen dos paralelos de contacto, lo que redunda en una menor distorsión de la zona proyectada.
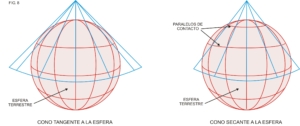
La ventaja más importante de este tipo de proyecciones radica en que la ortodrómica podría considerarse casi una recta con un error despreciable. La desventaja fundamental es que los rumbos loxodrómicos quedan representados por líneas curvas, razón por la cual no se utilizan en navegación.
- Proyecciones policónicas: Las cartas policónicas se contruyen a partir de superponer varias proyecciones cónicas puras, aunque difícilmente sean utilizadas con fines náuticos.
- Proyecciones cilíndricas: Dentro del grupo de las proyecciones por desarrollo podemos encontrar a las cilíndricas puras. Esta forma de representación, si bien en sí misma no sirve para la construcción de cartas náuticas, es la base fundamental de la proyección mercatoriana, la más utilizada en navegación. Y este será el tema de la próxima entrega.
Hasta la próxima
Darío G. Fernández
dfernandez@mastersailor.com.ar