Recordará el lector el viejo chiste que decía: “La tierra es redonda y la llamamos planeta, si fuese plana ¿la llamaríamos redondeta?” El dilema de la tierra redonda, plana o con forma de huevo, encierra en realidad un mito que nada tiene que ver con la realidad de la época de la conquista de América.
Seguramente a Ud., tanto como a mí, le habrán hecho creer en la escuela primaria que los debates entre el Almirante y los Reyes de España se basaban en demostrar que la tierra era redonda. Nada más alejado de la realidad. Todos los geógrafos y matemáticos que trabajaban para la corte de Isabel La Católica conocían esto a la perfección. De hecho, cualquier habitante de la España de aquella época, con suficiente grado de educación, lo sabía también.
Por aquellos años, la corona de España le encargó a un grupo de sabios el estudio sobre el viaje propuesto por Cristóbal Colón, quienes lo objetaron pero por otras razones. Ellos, al igual que Colón, sabían perfectamente que se podía llegar hasta las Indias, China y Japón navegando hacia el Oeste. La objeción no era entonces sobre la esfericidad terrestre. ¿Por qué se oponían entonces?
Se dice que los sabios alegaban, en contra del proyecto de Colón, que el perímetro terrestre era demasiado grande como para circunnavegarlo, razón por la cual no existiría embarcación que pudiese transportar la gran cantidad de víveres necesaria para una navegación tan extensa.
Por su parte, Cristóbal Colón decía que la Tierra no era tan grande y que sería sencillo el proyecto.
Pero ¿de qué lado estaba la verdad? ¿Colón estaba en lo cierto? ¿Eran los sabios los equivocados?
Nada de eso, el “Gran Almirante de toda la Mar Océana”, como gustaban de llamarlo sus allegados, cometía un grave error. Y si no hubiese tenido la fortuna de encontrarse con América, probablemente se habría perdido en alta mar y jamás se hubiese vuelto a saber de él.
LAS PRIMERAS CREENCIAS
Si bien hoy todos sabemos que la Tierra tiene forma “geoide”, muchas y muy variadas eran las creencias que tenían los pueblos antiguos en relación a su forma y al comportamiento de los astros que la rodean.
Algunos creían que el universo estaba formado por gigantes y dragones. En América, los aztecas sostenían que el Sol aparecía cada nuevo día provisto de un dardo luminoso para combatir y ahuyentar a la Luna (su hermana) y a las estrellas (sus hermanos), imponiendo así su reinado por el resto del día. Por la tarde moría regresando a la madre tierra, donde renovaba sus fuerzas para volver a combatir al día siguiente.

Los incas, por su parte, se consideraban descendientes del Sol.
Para las primitivas tribus de la India, la superficie terrestre era una inmensa bandeja sostenida por tres elefantes, los que a su vez estaban posados sobre una tortuga gigante. Admirable imaginación.
En el antiguo Egipto se pensaba en el cielo como en una visión del Nilo, a través del cual navegaba día a día el dios Ra (Sol), de Este a Oeste, regresando cada día a su punto de partida a través de los abismos subterráneos de la Tierra. Cada vez que un eclipse acontecía, decían que una serpiente había atacado a la embarcación que transportaba a su dios.
Hasta el siglo VI a.C. muchas fueron las creencias. Los primeros modelos cosmológicos de los griegos sostenían que la Tierra era plana.
Recién en el siglo VI a.C. Pitágoras, y más tarde Aristóteles (siglo IV a.C.), comienzan a argumentar a favor de la esfericidad terrestre.
LA REDONDEZ DE LA TIERRA
A pesar del gran retroceso cultural que sufrió la humanidad, está claro que Colón no descubrió la esfericidad de la Tierra ni mucho menos. Sencillamente se animó a constatar algo que, tanto Aristóteles como muchos otros, sabían perfectamente posible casi diecinueve siglos antes.
Aristóteles pudo comprobar ya en el siglo IV a.C. que la tierra era redonda basándose en sencillas observaciones:
- Cuando un barco se alejaba de puerto desaparecía el casco en primer lugar y luego sus velas.
- A medida que se viajaba al Norte, aumentaba la altura del polo Norte celeste.
- Al viajar hacia el Sur comenzaban a aparecer estrellas que hasta el momento se encontraban ocultas.
- Durante un eclipse de Luna, la sombra que la Tierra proyectaba sobre ésta era un arco de círculo, cosa que sólo podía ocurrir siendo la Tierra una esfera.
A pesar de sus avances, Aristóteles seguía creyendo que la Tierra ocupaba el centro del universo ya que no veía que las estrellas cambiaran su posición aparente entre sí. En realidad las estrellas sí modifican su posición aparente pero eso no podía ser detectado con los instrumentos de la época.
Se presume que Aristarco de Samos (siglo III a.C.) puso en duda todos los modelos de la época al proponer un universo cuyo centro era el Sol, aunque según parece no fue tenido muy en cuenta.
Hiparco de Samos (siglo II a.C.), uno de los más grandes astrónomos de la época, pudo calcular con una exactitud asombrosa la distancia entre la Tierra y la Luna y creó el primer catálogo de estrellas que se conoce, dando a cada una un valor de “magnitud” según su brillo que aún hoy continúa vigente.
Claudios Ptolemaios (más conocido por Tolomeo), fue el último gran astrónomo griego. Vivió durante la mayor parte de su vida en Alejandría (Egipto) en el 150 a.C. aproximadamente. Desarrolló a través de los años un modelo de universo basado en las observaciones de Hiparco y fundamentado con conceptos matemáticos muy detallados. El “Universo de Tolomeo” pone a la Tierra como centro del universo conocido, y al Sol, Luna, planetas y estrellas girando en torno a ésta en órbitas circulares y a velocidades constantes. Toda su obra fue compilada en un libro que se llamó “Almagesto”.
Hasta aquí, a nadie se le ha ocurrido pensar que la Tierra era plana.
Posterior a Tolomeo, nada nuevo sino hasta mil años después en que Nicolás Copérnico y Tycho Brahe (siglo XVI d.C.) aportaron nuevas ideas basadas en los estudios que, a partir del legado de Tolomeo, continuaron los árabes.
Copérnico, hombre de la iglesia, se atrevió a desafiar el concepto tolemaico y a la iglesia misma colocando al Sol en el centro del universo, lo que le valió algunos problemas.
Tycho, por su parte, basándose en los modelos de Tolomeo y de Copérnico, decidió efectuar las mediciones más precisas hechas hasta el momento e instaló el observatorio más avanzado que se conocía. La exactitud de las observaciones efectuadas por Tycho Brahe ha revolucionado la astronomía de la época.
Estando en Praga, Tycho contrató a un asistente para que colaborara con sus observaciones, nada menos que al alemán Johannes Kepler (1571-1630). El gran aporte de este genial astrónomo y matemático fue el de reemplazar a las órbitas circulares por “elipses”, formulando las tres famosas leyes sobre el movimiento planetario que aún hoy se estudian y son completamente vigentes.
Si bien es cierto que Copérnico era contemporáneo a Don Cristóbal y que Tycho y los demás fueron posteriores, a nadie se le ocurría que la Tierra pudiese ser plana desde hacía por lo menos mil ochocientos años. ¿Curioso no?
Esto no es todo. No sólo que se sabía perfectamente de la redondez de la Tierra sino que, para completar el cuadro, uno de los grandes filósofos del período griego se empecinó en querer calcular su radio. Lo increíble es que lo logró y con una exactitud que asombra.
EL RADIO TERRESTRE
Eratóstenes (275 – 194 a.C.) nació en la ciudad de Cyrene y pasó la mayor parte de su vida en Atenas. Notable como geógrafo, poeta, filósofo y matemático, pasó a la inmortalidad a partir de haber sido el primero en medir el radio terrestre.
El método que utilizó es increíblemente sencillo (FIG. 1) :

Figura 1
Sabía que durante el solsticio de verano, en un pozo ubicado en la ciudad de Alejandría los rayos solares iluminaban completamente el fondo de dicho pozo. Razonó entonces que en ese momento, el Sol se encontraba exactamente sobre la vertical del lugar.
Contrató entonces a un caminante que pudiera cotejar (a pie) la distancia entre ese lugar y una torre ubicada en la ciudad de Syene. Se dijo así mismo que, dada la enorme distancia que separa a la Tierra del Sol, los rayos luminosos de éste deberían caer paralelos entre sí en cualquier lugar de la Tierra. Por lo tanto, si ésta fuese plana, el mismo día y a la misma hora el Sol debería encontrarse también sobre la ciudad de Syene en forma perfectamente vertical. Si esto fuese así, la sombra que la torre de Syene proyectaría sobre el suelo debería ser nula, cosa que no ocurrió.
Sucedió lo esperado, la torre de Syene, dada la curvatura terrestre, no guardaba la misma verticalidad que el pozo de Alejandría, sino que entre ambos había cierto ángulo.
Sencillamente midió el ángulo que formaba la sombra de la torre, que sin lugar a dudas es el mismo que se mediría desde el centro de la tierra entre ambos objetos (el pozo y la torre): siete grados (7º).
A su vez, el caminante enviado regresó con la novedad de que entre ambos lugares había 800 kilómetros de distancia.
Lo que quedaba era realmente sencillo:
Si 7º de circunferencia terrestre equivalen a 800 kilómetros, entonces los 360º del perímetro terrestre tendrían que alcanzar una cifra cercana a los 41.000 kilómetros.
7º ________________ 800 km.
360º ______________ (360 x 800) / 7
En realidad, en aquella época no se utilizaban los kilómetros para medir distancias sino los “estadios” que tomaban como unidad de medida la longitud del estadio olímpico. El valor del “estadio” se presta a controversias.
Eratóstenes determinó la distancia entre Syene y Alejandría en 252.000 estadios. De adoptar el valor del estadio sugerido por Plinio, en 157,5 metros, el error cometido por Eratóstenes sería tan sólo de 80 kilómetros. Nada mal ¿verdad?
UN EXPERIMENTO CASERO
La experiencia de Eratóstenes me da pie para sugerirle un sencillo experimento casero a fin de determinar con suma exactitud los 4 puntos cardinales con la ayuda de tan solo una varilla cualquiera (FIG: 2). Esto por supuesto en el caso que a Ud. le interese trazarlos en su casa por alguna razón en particular, por ejemplo para ubicar una veleta, para trabajar con algún telescopio, para instalar un reloj de sol (que en algún número le enseñará cómo hacerlo), o bien porque no tiene otra cosa mejor que hacer. Ni se le ocurra intentar hacerlo en navegación porque los resultados serían desastrosos.

Figura 2
Para empezar, busque un rincón de su casa donde incida el Sol cerca del mediodía, un rato antes y un rato después. Previo al mediodía instale la varilla en el suelo o sobre alguna mesa lo más vertical que pueda y trace la sombra que ésta proyecta con un lápiz. Mida la longitud de la línea trazada.
Notará que a medida que pasa el tiempo la longitud de la sombra se va acortando, alcanzando su mínima longitud exactamente cuando el Sol atraviesa por el meridiano del lugar. A partir de ese instante, la sombra volverá a estirarse nuevamente. Espere hasta que la sombra proyectada vuelva a tener la misma longitud que la que midió al principio, y vuelva a trazarla.
Una luego los dos extremos de las líneas trazadas formando un triángulo.
Divida esta línea por la mitad y una ese punto con el vértice del triángulo. Ha trazado usted la “meridiana” del lugar, al igual que quien lo hace con un sextante.
La línea trazada apunta al Norte y al Sur. Si quiere los demás puntos cardinales, simplemente trace una perpendicular a dicha línea.
Los astros “culminan” alcanzando su máxima altura respecto del horizonte cuando atraviesan el meridiano del lugar. En el caso del Sol, cuando esto ocurre, la sombra proyectada será la más pequeña. Lo que hicimos fue simplemente encontrar la línea en que la sombra proyectada por el Sol era la más corta, por lo tanto hallamos el meridiano del lugar.
CALCULEMOS LA LATITUD
Este método permite también calcular la latitud del lugar, claro que para ello es preciso conocer la declinación del Sol (equivalente a la latitud) para ese día, dato que puede obtenerse del Almanaque Náutico, o bien de la página oficial del Servicio de Hidrografía Naval (FIG. 3).
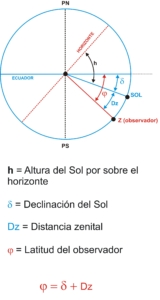
Figura 3
En el gráfico se puede apreciar al Sol en el momento de su “culminación” respecto del observador “Z”, o sea cuando atraviesa su meridiano.
Sin entrar en consideraciones demasiado complejas, la latitud del observador (Z) surge, en este caso puntual, de sumar la declinación del Sol y la distancia zenital al mismo. Para aclarar un poco las cosas diremos que la altura (h) de un astro cualquiera queda definida por el ángulo formado entre el horizonte y la visual al astro en cuestión. A su vez, la distancia zenital (Dz) es el ángulo formado entre la visual a dicho astro y el zenit del observador. Dado que entre el horizonte y el zenit hay 90º, la distancia zenital será igual a 90º – h.
Como dijimos anteriormente, la declinación la obtenemos del Almanaque Náutico y la distancia zenital la acabamos de medir casi sin darnos cuenta. Es, en definitiva, el ángulo que forma el extremo superior de la varilla y la línea media del triángulo formado por la sombra proyectada. El mismo ángulo que midió Eratóstenes (FIG 4).
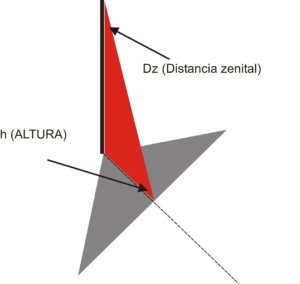
Figura 4
Sólo resta hacer el cálculo.
Téngase en cuenta que la fórmula es válida solo en el caso que el observador y el Sol guarden entre sí las posiciones relativas de la figura anterior. Para otros casos, habrá que deducir la fórmula construyendo un nuevo esquema.
Bueno, tal vez nos hayamos corrido un poco del tema central de esta nota. Lo cierto es que, según parece, la Tierra era redonda. ¿Hasta cuando van a seguir insistiendo con la historia del huevo?
Ah, me olvidaba. La palabra “Planeta” proviene del griego (Planetai) y quiere decir “errante”. Los planetas recibieron ese nombre en alusión al lento movimiento que éstos describen respecto de las estrellas. Así que, aunque la Tierra sea redonda, podemos continuar llamándola “Planeta”.
Hasta la próxima…
Darío G. Fernández | Director del ISNDF



