Continuando con lo visto hasta aquí y para cerrar esta seguidilla de artículos sobre faros, vamos a repasar los procedimientos más comunes, y a la vez más utilizados, para determinar la distancia a un objeto a partir del conocimiento de su altura sobre el nivel del mar. Aquí pueden darse dos casos bien definidos: que el faro se aprecie en su totalidad dentro del horizonte o bien que, debido a la curvatura terrestre, solo pueda verse una porción del mismo, quedando oculta su base tras el horizonte marino. Los procedimientos a utilizar son bien distintos en cada caso y esto es lo que veremos a continuación.
DISTANCIA A UN OBJETO DE ALTURA CONOCIDA SITUADO DENTRO DEL HORIZONTE
Como ya habíamos mencionado en anteriores notas, este caso se da cuando la distancia al objeto en cuestión es menor a la distancia del observador al horizonte y, por lo tanto, el faro se visualiza en su totalidad. Para resolver el cálculo, una vez medida la altura angular entre el tope y la base, pueden utilizarse dos procedimientos igual de válidos. El primero es muy sencillo y se basa en la aplicación de los conceptos básicos de la trigonometría.
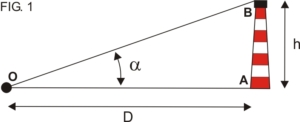
En la figura Nº 1 puede apreciarse cómo, entre el ojo de observación (O), la base del faro (A) y su tope (B), queda conformado el triángulo rectángulo (ABC), donde:
- “h” representa la altura real del objeto.
- “a” es su altura angular, es decir el ángulo medido por el observador entre la base y el tope del faro (sextante).
- “D” es la distancia a la que se encuentra el objeto del punto de observación y es precisamente lo que se pretende determinar.
Una manera simple de resolverlo es aplicando una función trigonométrica que relacione a los tres elementos que acabamos de mencionar. En este caso, la mejor es la función tangente. Si recuerda el lector, la tangente de un ángulo es igual al cateto opuesto sobre el cateto adyacente, es decir:
\textrm{tg}\,\; \alpha = \frac{\textrm{Cat. opuesto}}{\textrm{Cat. adyacente}}=\frac{\textrm{AB}}{\textrm{AO}}=\frac{\textrm{h}}{\textrm{D}}Por lo tanto:
D = \frac{h}{\textrm{tg}\,\; \alpha}O bien:
D = h \times \textrm{cotg}\, \; \alphaEn la fórmula anterior, a deberá expresarse en grados y fracción. En cuanto a la altura, si su valor se introduce en metros, el valor de la distancia obtenido será también en metros. Para expresar esto mismo en millas náuticas, solo habrá que dividir el resultado por 1.853, quedando la fórmula final de la siguiente manera:
D_{millas}= \frac{h(metros)\times cot\; \alpha}{1.852}
A fin de que el procedimiento resulte más claro para el lector, proponemos un sencillo ejercicio:
- ¿A qué distancia me encontraré de un faro; que se encuentra situado dentro del horizonte, cuya altura medida por medio del sextante es de 1º 25’ de arco y su altura real sobre el nivel del mar es de 94 metros?
Reemplazando los valores en la fórmula tenemos:
D_{millas}= \frac{94\; metros \times cot\; 1^{\circ}\; 25}{1.852}
D_{millas}= 2,05\; Mn
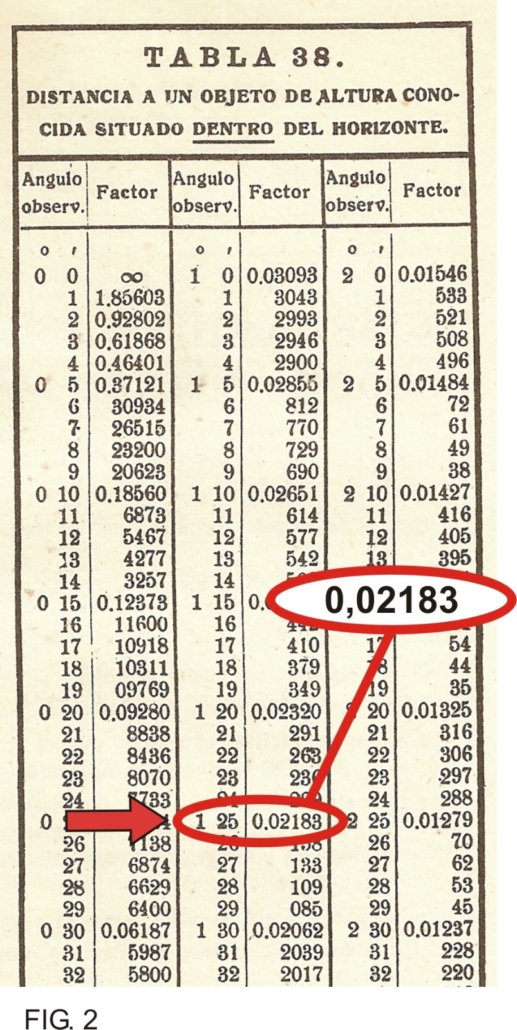
Esto mismo puede hacerse utilizando determinadas tablas que ya traen los resultados tabulados para distintos valores, tanto de altura observada como de altura real del objeto.
Las tablas representan exactamente la fórmula anterior:
D_{millas}= \frac{h(metros)\times cot\; \alpha}{1.852}
Pero dan solamente el valor del factor (F)
F=\frac{cot\; \alpha }{1.852}
Una vez obtenido “F” de la tabla, solamente resta multiplicarlo por el valor de la altura del faro (H)
D (millas) = h (metros) x F
Para ejemplificar su uso, tomemos como ejemplo el ejercicio anterior:
1) Ingresamos a la tabla por la columna “Angulo observado” con el valor obtenido por medio del sextante (1º 25’) y extraemos el factor (F): 0,02183.
2) Multiplicamos el factor por la altura en metros del objeto (94 metros):
D (millas) = 94 mts. x 0,02183
D (millas) = 2,05 Mn.
Como puede apreciarse, hemos arribado a idéntico resultado.
Existe otra manera de llevar adelante el mismo cálculo. Aplicaremos en este caso otra unidad que, al igual que sucede con los grados, minutos y segundos, también se utiliza para expresar el valor de un ángulo determinado: el radián.
El radián surge del cociente entre el arco de circunferencia que subtiende un ángulo determinado (curva), y el radio que limita a dicha circunferencia (recta). Cuando la longitud del arco es igual a la del radio, el ángulo en cuestión es de 1 radián. El símbolo utilizado es “rad”.
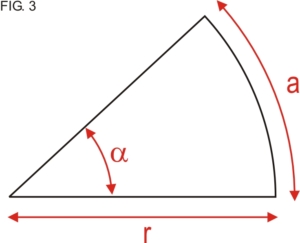
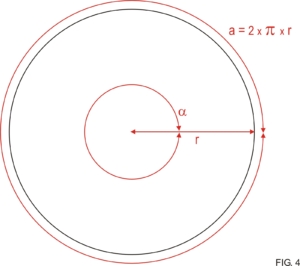
Ahora bien, ¿A cuántos grados equivale un radián? Para averiguarlo supondremos un ángulo de 360º, es decir una circunferencia. Fig. 4.
Aplicamos la fórmula:
\alpha =\frac{a}{r}En este caso, por ser el ángulo de 360º, el arco es todo el perímetro de la circunferencia, o sea 2.p.r.
\alpha =\frac{2\; \times \pi \times \not{r}}{\not{r}}Simplificando “r” arriba y abajo:
a = 2 x p = 2 x 3,14
Por lo tanto:
360º = 6,28 rad
1\; rad = \frac{1\times 360}{6,28}1 rad = 57,32º = 3.439’
Ahora bien, si aplicamos el mismo procedimiento que el del primer caso (ver figura 1), pero esta vez utilizando el concepto de radianes, tendremos que:
\alpha _{(rad)}=\frac{h(metros)}{D(metros))}Pero si a lo quiero expresar en minutos, entonces:
D _{(minutos)}=\frac{h(metros)}{D(metros))}\times 3.439Entonces:
D _{(metros)}=\frac{h(metros)}{\alpha(minutos)}\times 3.439Y si quiero expresar la distancia en millas:
D _{(millas)}=\frac{h(metros)}{\alpha(minutos)}\times \frac{3.439}{1.852}Por lo tanto, la fórmula definitiva para el cálculo de la altura a un faro que se ve dentro del horizonte será:
D_{(millas)}=\frac{h(metros)}{\alpha(minutos)}\times 1,86Para comprobarlo, reemplacemos en la fórmula los valores del ejercicio propuesto anteriormente. Téngase en cuenta que, en este caso, deberá ingresarse con el valor de la altura angular expresado en minutos (1º 25’ = 85’)
D_{(millas)}=\frac{94\; metros}{85\; minutos}\times 1,86D (millas) = 2,05 Mn.
El resultado sigue siendo el mismo.
DISTANCIA A UN OBJETO DE ALTURA CONOCIDA SITUADO MÁS ALLÁ DEL HORIZONTE
Como ya dijimos con anterioridad, éste es el caso en el cual la curvatura terrestre no deja ver el faro por completo. Por ende, con el sextante solo podrá medirse la altura de una determinada porción del mismo, entre su tope y el horizonte marino. Fig. 5.
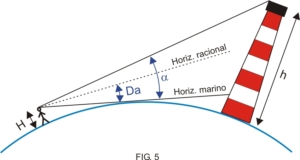
- “H” es la altura de ojo del observador.
- “h” es la altura del faro.
- “a” es la altura angular medida con el sextante entre el tope del objeto y el horizonte marino.
- “Da” es la depresión aparente entre el horizonte racional (horizontal) y el horizonte marino, producto de la altura de ojo del observador.
Este procedimiento es un tanto más complejo que los anteriores ya que son más las variables en juego. Existen varias fórmulas que posibilitan hacer el cálculo, pero dada su complejidad, nos remitiremos a hacerlo por medio de tablas. Entre ellas, la más conocida es la tabla 39, que aparece publicada en los libros de la Escuela Naval Militar bajo el título “Distancia a un objeto de altura conocida situado más allá del horizonte”. Fig. 6.
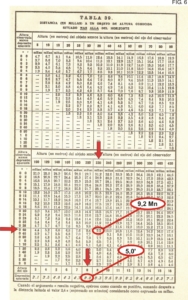
Los argumentos para ingresar a la tabla son dos:
- Por la columna de la izquierda se entra con el valor de la altura observada (a) menos la depresión aparente (Da). Al pie de la tabla se puede obtener este último ingresando con la altura de ojo del observador.
- Por la parte superior se ingresa con el valor de la altura en metros del objeto (h) menos la altura de ojo del observador (H).
Para comprender mejor su uso, veamos un ejemplo:
2) Determinar a que distancia se encontrará de un faro, cuya altura sobre el nivel del mar (h) es de 228 metros, un observador que ha tomado una altura con su sextante (a) de 0º 45’, desde una altura de ojo (H) de 8 metros.
En primer lugar extraemos del pie de la tabla el valor de la depresión aparente para una elevación de ojo de 8 metros:
Da = 5,0’
Calculamos la diferencia entre la altura observada y la depresión aparente, cuyo resultado servirá como argumento de entrada a la tabla:
a – Da = 0º 45’ – 5’ = 0º 40’
Hacemos lo propio con el otro argumento de entrada (altura del objeto – altura de ojo):
h – H = 228 metros – 8 metros = 220 metros
Hecho esto, ingresamos a la tabla por la columna de la izquierda con el argumento “a – Da” (0º 40’) y por la parte superior con “h – H” (220 metros). De la intersección entre fila y columna obtenemos el resultado final de la distancia al faro:
D = 9,2 Mn.
Aclaración Importante: Para saber qué procedimiento efectuar en cada caso es preciso saber si el objeto en cuestión se encuentra situado “dentro” o “más allá” del horizonte. Para determinarlo se procederá de la siguiente manera:
- Se calcula la distancia al horizonte como vimos en el número anterior, aplicando la fórmula o por tablas.
- Se determina la distancia al faro como si éste se encontrase dentro del horizonte, con cualquiera de los sistemas vistos anteriormente.
- Si la distancia al horizonte resulta mayor que la distancia al objeto, esto significa que dicho objeto se encuentra dentro del horizonte y se dará por válido el cálculo anterior.
- Si la distancia al horizonte resulta menor que la distancia al objeto, el mismo se encontrará situado más allá del horizonte y deberá aplicarse dicho procedimiento para determinar la distancia.
Fe de erratas: En la parte II de esta nota, publicada en el newsletter anterior, se deslizaron involuntariamente algunos errores de signos, a saber:
Donde dice: \sqrt{2\times R}\;\; \sqrt{H}; Debe decir: \sqrt{2\times R}\; \times \sqrt{H}
Donde dice: \sqrt{2\times 6.370.000}\;\;\sqrt{H}; Debe decir: \sqrt{2\times 6.370.000}\;\times \;\sqrt{H}
Donde dice: \sqrt{\frac{2\times 6.370.000}{1 - 2\times 0,08}}\; \;\sqrt{H}; Debe decir: \sqrt{\frac{2\times 6.370.000}{1 - 2\times 0,08}}\;\times \;\sqrt{H}
Darío G. Fernández | Director del ISNDF | dfernandez@isndf.com.ar



